 The researchers and engineers studying quantum technologies are exploring uncharted territory. Due to the unintuitive quirks of quantum physics, the terrain isn’t easy to scout, and the path of progress has been littered with wrong turns and dead ends.
The researchers and engineers studying quantum technologies are exploring uncharted territory. Due to the unintuitive quirks of quantum physics, the terrain isn’t easy to scout, and the path of progress has been littered with wrong turns and dead ends.
Sometimes, though, theorists have streamlined progress by spotting roadblocks in the distance or identifying the rules of the road. For instance, researchers have found several quantum speed limits—called Lieb-Robinson bounds—that are impassable caps on how quickly information can travel through collections of quantum particles. They’ve even developed protocols for quantum computers that achieve the best possible speeds for specific cases. But to make calculating the limits easier, physicists have mostly neglected the influence of disorder. In the real world, disorder can’t always be ignored, so researchers need to understand its potential effects.
University of Maryland researchers including Alexey Gorshkov (in photo), a fellow in the Joint Center for Quantum Information and Computer Science (QuICS), are facing down the impact disorder has on speed limits.
In an article published in June 2023 in the journal Physical Review X Quantum, Gorshkov—joined by researchers in the Joint Quantum Institute (JQI) including Chris Baldwin, a former postdoctoral scholar at Maryland who is now an assistant professor at Michigan State University—described novel methods for pulling insights from the mess created by disorder and identified new types of quantum speed limits that apply when disorder is present.
"We were motivated both by the beautiful theoretical problem of proving and saturating new speed limits and by the implications that our work would have on quantum computers that inevitably have some disorder," says Gorshkov, who is also a physicist at the National Institute of Standards and Technology and a fellow in JQI.
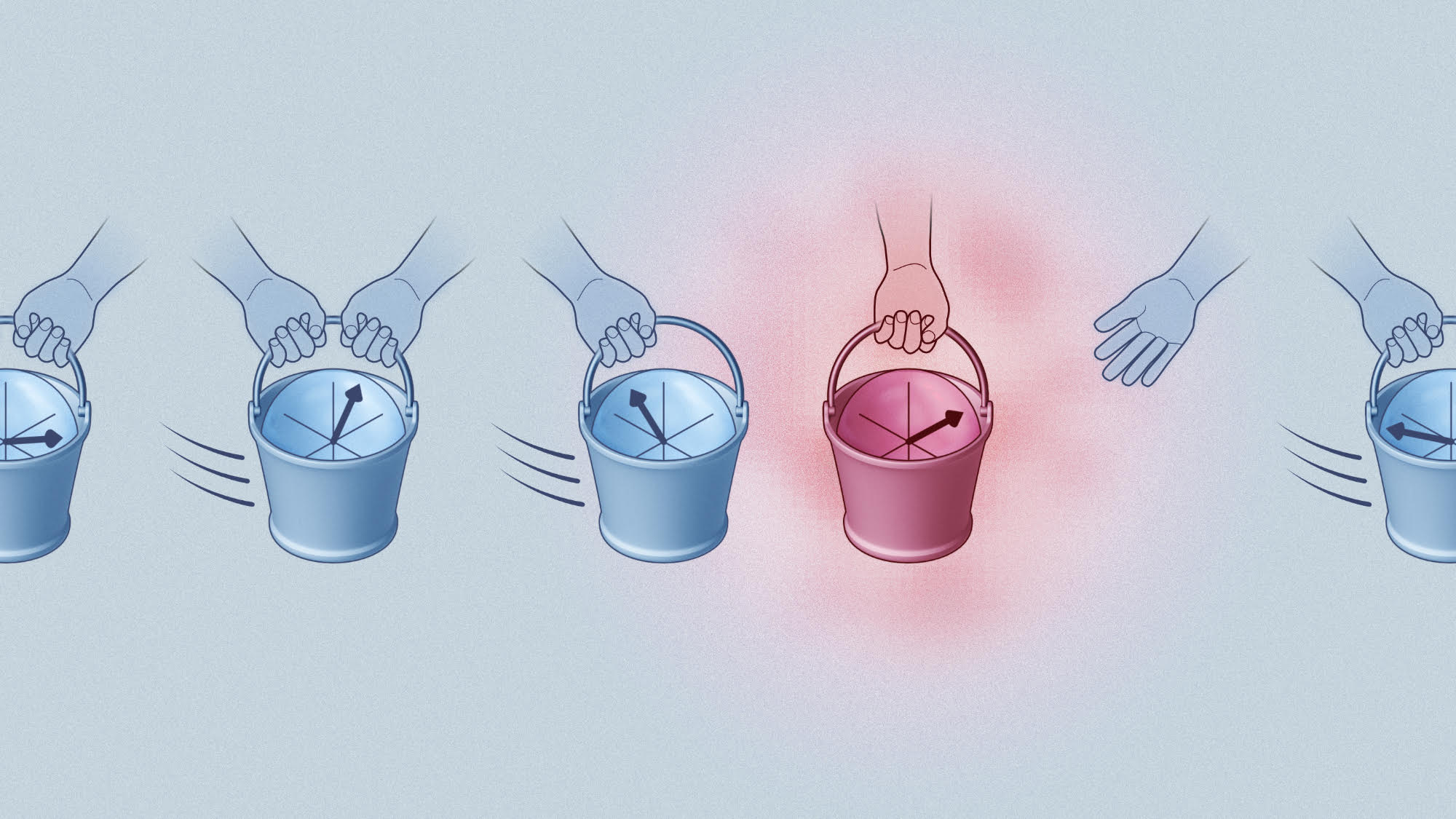 A chain of quantum spins can pass information down a line like a bucket brigade, but sometimes disorder (represented here by the red hand and bucket) can slow down the communication. The arrows in spheres in the buckets are a geometrical representation of a quantum state. Image credit: Sean Kelley/NIST.
A chain of quantum spins can pass information down a line like a bucket brigade, but sometimes disorder (represented here by the red hand and bucket) can slow down the communication. The arrows in spheres in the buckets are a geometrical representation of a quantum state. Image credit: Sean Kelley/NIST.
Baldwin (lead author of the paper), Gorshkov and colleagues began by tackling the case of a one-dimensional line of particles, where each particle can only directly interact with its neighbors. They specifically focused on the spin—a quantum property related to magnetism—of each quantum particle. A spin is like a compass needle that wants to point along a magnetic field, but, being quantum, it can point in more than one direction at a time—a phenomenon called superposition.
Spins pass information to each other through interactions, so a line of spins can act like a bucket brigade passing quantum information: One jiggles its neighbor, which jiggles its neighbor on the other side, and the information makes its way down the line.
But if something is slightly off about a spin’s connection to a neighbor—there’s some disorder—the spin will fumble handing over the quantum data and slow things down. With their imperfect handovers, spins resemble people in a bucket brigade each working at a slightly different speed. Most people probably take a similar amount of time to pass a bucket, maybe clustered around a couple of seconds. But if enough random people are pulled in, a few speed demons may only need a second while others might take five seconds or more.
To account for the full range of possibilities in quantum systems, Baldwin and colleagues didn’t limit themselves to a fixed number of possible speeds. Instead, they analyzed distributions of speeds that extend from the quickest transfers for ideal connections between spins down infinitely to even the slightest chances of handoffs taking millennia or longer for arbitrarily bad connections. In future quantum computers, experts expect millions of spins to work together. With so many spins, even long odds of any individual being a slowpoke can combine into a safe bet that one, or even several, will be present.
To make sense of the sea of possibilities presented by disorder’s influence on handoff speeds, Baldwin and colleagues pulled out the tools of probability theory. These tools allowed them to glean information about speed limits from the statistics of how transfer speeds are peppered throughout the line. With probability theory, they derived new speed limits for whole groups of spin chains based on the big picture without needing to know anything about the links between any particular spins.
The team was particularly interested in investigating if the speeds information can reach in different systems depend on the distance it is traveling. Some physical processes, like light travelling through space, resemble a car steadily cruising down an empty highway, where the travel time is directly proportional to the distance—it takes twice as long to move twice as far. But the speeds of other processes, like perfume defusing through a room, don’t have such a straightforward proportional behavior and can look more like a flagging runner who takes longer and longer the farther they push themselves. Knowing the relationship between speed and distance for quantum information is valuable when researchers are weighing their options for scaling up quantum computers.
With their new results, the researchers determined that information can’t always propagate at a steady speed indefinitely, and they identified the border between conditions that allow a steady speed from those that only allow a deteriorating pace.
They also found that their method allowed them to define two distinct types of limits that tell them different things. One they dubbed “almost always bounds” because the bounds hold for almost all the sections of a chain. These limits apply to any sufficiently long stretch of spins even though they might occasionally be violated for small sections of the chain—like if there is an unusual clump of speed demons in the brigade. These limits allow researchers to guarantee conditions, like that a particular spin won’t be disturbed by activity further down the line within a particular time window.
The researchers called the second type of limit “infinitely often bounds” because they are guaranteed to apply to some stretches of an infinite chain but there isn’t a guarantee that the limit will definitely hold for any particular stretch no matter how long a section is being considered. So, these limits are expected to occasionally pop up on sections of the chain and generally lower the limit from that set by the almost always bound—like a car occasionally entering a work zone on the highway. Having an idea of these lower speed limits that are likely to pop up can help researchers to judge the reasonable minimum amount of time to dedicate to getting the bucket all the way across a stretch of the brigade.
The newly defined limits allowed the team members to resolve a lingering discrepancy: The existing Lieb-Robinson bounds had set a higher ceiling than any information transfer protocol had reached. The mismatch could have been the result of either researchers not being creative enough in designing the protocols or them failing to account for something that enforced a lower limit. Accounting for disorder more carefully dropped the theoretical ceiling down to match the speed of existing protocols.
“For a while, we had this gap,” Baldwin says. “The main exciting thing of this work was figuring out how we could completely close this gap.”
The researchers say there is further work to be done exploring the applications of these limits and determining when the two types of bounds have significant impacts.
“The main direction I want to take this going forward is going beyond one dimension,” Baldwin says. “My suspicion is that the picture will end up looking very different, but I think it's still worth having this one-dimensional case in mind when we start to do that.”
—Story by Bailey Bedford, JQI communications group