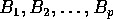 , and a permutation
, and a permutation 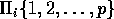 , and
, and 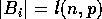 , block
, block 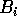 has to be moved
from
has to be moved
from 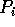 to
to 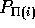 . If each block has length
. If each block has length 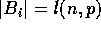 , we claim that the CM-5 time complexity of this operation is
the following:
, we claim that the CM-5 time complexity of this operation is
the following:
As described in Subsection 2.1, we use
(1) as the general model for CM-5 communications. As
stated above, a common communications pattern on parallel machines is
a block permutation, where given blocks of contiguous data 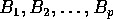 , and a permutation
, and a permutation 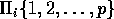 , and
, and 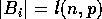 , block
, block 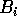 has to be moved
from
has to be moved
from 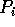 to
to 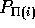 . If each block has length
. If each block has length 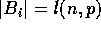 , we claim that the CM-5 time complexity of this operation is
the following:
, we claim that the CM-5 time complexity of this operation is
the following:
Each node in the CM-5 connects to the fat-tree via a 20 Mb/sec network interface link [34]. The fat-tree network provides sufficient bandwidth to allow every node to perform sustained data transfers at a rate of 20 Mb/sec if all communications is contained in groups of four nodes (i.e. the nodes differ only in the last two bits of their logical address), 10 Mb/sec for transfers within groups of 16 nodes (i.e. the nodes differ in only the last four bits), and 5 Mb/sec for all other communication paths in the system [34].
A regular grid shift is an example of a block permutation pattern of
data movement as shown in Subsection 2.2.2. For the
corresponding regular block communications, the CM-5 can achieve
bandwidths of 15 megabytes/sec per processor to put messages into and
take messages out of the data network [29]. The runtime
system (RTS) of the CM-5 will choose a data section for a message of
between 1 and 5 words in length. If we assume that the data section
of a message, 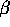 , is four 4-byte words, and the header and
trailer are an additional 4 bytes, then
, is four 4-byte words, and the header and
trailer are an additional 4 bytes, then 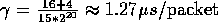 .
.
To support these claims, we give the following empirical results.
Using the message passing library of the CM-5, CMMD version 3.0
[41], each processing node swaps a packet with another
node of fixed distance away. Figure 3 confirms that
there is a linear relationship between message length and total
transmission time on the CM-5. We find that when the regular block
permutation consists of only local communications, i.e. messages are
contained in each cluster of four leaf nodes, 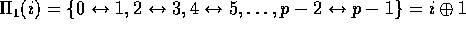 , the lower bound on time is obtained.
A least squares analysis of this data finds
, the lower bound on time is obtained.
A least squares analysis of this data finds 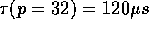 and
and 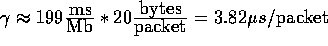 . This
is equivalent to a sustained transfer rate of 5.03 Mb/sec.
. This
is equivalent to a sustained transfer rate of 5.03 Mb/sec.
Other regular block permutations are shown in Figure 3 such as
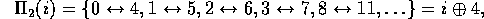
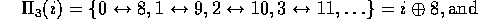
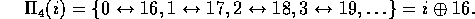
Both 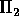 and
and
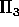 use two levels of the fat-tree, while
use two levels of the fat-tree, while 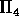 needs three
levels. Our results show that all non-local regular permutations
routed through the fat-tree have similar time complexities, with
needs three
levels. Our results show that all non-local regular permutations
routed through the fat-tree have similar time complexities, with 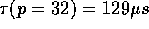 and
and 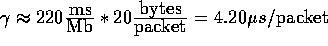 . This
corresponds to a sustained transfer rate of 4.55 Mb/sec.
. This
corresponds to a sustained transfer rate of 4.55 Mb/sec.
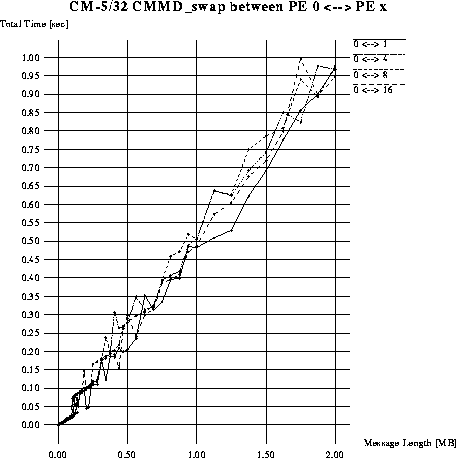
Figure: Sending Time of a Regular Block Permutation