


Next: Parallel Algorithm Analysis
Up: Scalable Data Parallel Algorithms
Previous: Scalable Data Parallel Algorithms
Random Fields have been successfully used to sample and synthesize
textured images ([14], [10], [24],
[21], [17], [32], [12],
[11], [15], [18], [9],
[37], [6], [7], [8]).
Texture analysis has applications in image segmentation and
classification, biomedical image analysis, and automatic detection of
surface defects. Of particular interest are the models that specify
the statistical dependence of the gray level at a pixel on those of
its neighborhood. There are several well-known algorithms describing
the sampling process for generating synthetic textured images, and
algorithms that yield an estimate of the parameters of the assumed
random process given a textured image. Impressive results related to
real-world imagery have appeared in the literature ([14],
[17], [12], [18], [37],
[6], [7], [8]). However, all
these algorithms are quite computationally demanding because they
typically require on the order of 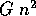 arithmetic operations
per iteration for an image of size
arithmetic operations
per iteration for an image of size 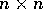 with G gray levels.
The implementations known to the authors are slow and operate on
images of size
with G gray levels.
The implementations known to the authors are slow and operate on
images of size 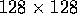 or smaller. Recently, a parallel
implementation has been developed on a DAP 510 computer
[21]. However, the DAP requires the structure of the
algorithms to match its topology, and hence the corresponding
algorithms are not as machine-independent as the algorithms described
in this paper. In addition, we show that our algorithms are scalable
in machine size and problem size.
or smaller. Recently, a parallel
implementation has been developed on a DAP 510 computer
[21]. However, the DAP requires the structure of the
algorithms to match its topology, and hence the corresponding
algorithms are not as machine-independent as the algorithms described
in this paper. In addition, we show that our algorithms are scalable
in machine size and problem size.
In this paper, we develop scalable data parallel algorithms for
implementing the most important texture sampling and synthesis
algorithms. The data parallel model is an architecture-independent
programming model that allows an arbitrary number of virtual
processors to operate on large amounts of data in parallel. This
model has been shown to be efficiently implementable on both SIMD
(Single Instruction stream, Multiple Data stream) or MIMD (Multiple
Instruction stream, Multiple Data stream) machines, shared-memory or
distributed-memory architectures, and is currently supported by
several programming languages including
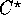 , data-parallel C, Fortran 90, Fortran D, and
CM Fortran. All our algorithms are scalable in terms of the number of
processors and the size of the problem. All the algorithms described
in this paper have been implemented and thoroughly tested on a
Connection Machine CM-2 and a Connection Machine CM-5.
, data-parallel C, Fortran 90, Fortran D, and
CM Fortran. All our algorithms are scalable in terms of the number of
processors and the size of the problem. All the algorithms described
in this paper have been implemented and thoroughly tested on a
Connection Machine CM-2 and a Connection Machine CM-5.
The Thinking Machines CM-2 is an SIMD machine with 64K bit-serial
processing elements (maximal configuration). This machine has 32 1-bit
processors grouped into a Sprint node to accelerate
floating-point computations, and 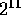 Sprint nodes are
configured as an 11-dimensional hypercube. See
Figure 1 for the organization of a Sprint node.
Sprint nodes are
configured as an 11-dimensional hypercube. See
Figure 1 for the organization of a Sprint node.
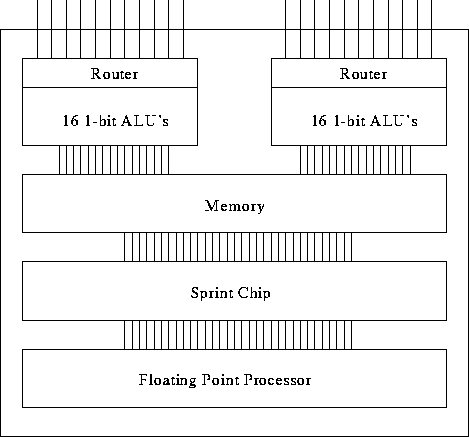
Figure: The organization of a CM-2 Sprint node
The Thinking Machines CM-5 is a massively parallel computer with
configurations containing 16 to 16,384 sparc processing nodes, each of
which has four vector units, and the nodes are connected via a
fat-tree communications network. The CM-5 is an MIMD machine which
can run in Single Program Multiple Data (SPMD) mode to simulate SIMD
operation. An in-depth look at the network architecture of this
machine is described in [29]. The nodes operate in parallel
and are interconnected by a fat-tree data network. The fat-tree
resembles a quad-tree, with each processing node (PN) as a leaf and
data routers at all internal connections. In addition, the bandwidth
of the fat-tree increases as you move up the levels of the tree
towards the root. Leiserson ([28]) discusses the benefits
of the fat-tree routing network, and Greenberg and Leiserson
([19]) bound the time for communications by randomized
routing on the fat-tree. In this paper, we assume the Single Program
Multiple Data (SPMD) model of the CM-5, using the data parallel
language 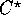 . In the SPMD model, each processing node executes a
portion of the same program, but local memory and machine state can
vary across the processors. The SPMD model efficiently simulates the
data parallel SIMD model normally associated with massively parallel
programming. References [40] and
[34] provide an overview for the CM-5, and both [43]\
and [45] contain detailed descriptions of the data parallel
platform. Note that a CM-5 machine with vector units has four vector
units per node, and the analysis given here will remain the same. See
Figure 2 for the general organization of the CM-5 with
vector units.
. In the SPMD model, each processing node executes a
portion of the same program, but local memory and machine state can
vary across the processors. The SPMD model efficiently simulates the
data parallel SIMD model normally associated with massively parallel
programming. References [40] and
[34] provide an overview for the CM-5, and both [43]\
and [45] contain detailed descriptions of the data parallel
platform. Note that a CM-5 machine with vector units has four vector
units per node, and the analysis given here will remain the same. See
Figure 2 for the general organization of the CM-5 with
vector units.
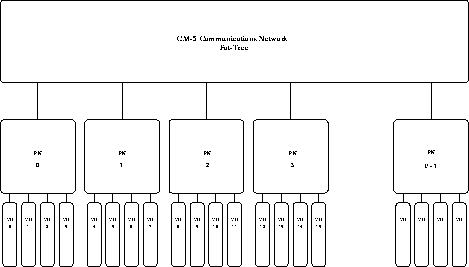
Figure: The organization of the CM-5
This paper addresses a simple image processing problem of texture
synthesis and compression using a Gibbs sampler as an example to show
that these algorithms are indeed scalable and fast on parallel
machines. Gibbs sampler and its variants are useful primitives for
larger applications such as image compression
([8], [27]), image estimation
([18], [21], [37]), and texture segmentation
([32], [15], [12], [16], [13]).
Section 2 presents our model for data parallel algorithm
analysis on both the CM-2 and the CM-5. In Section 3,
we develop parallel algorithms for texture synthesis using Gibbs and
Gaussian Markov Random Fields. Parameter estimation for Gaussian
Markov Random Field textures, using least squares, as well as maximum
likelihood techniques, are given in Section 4.
Section 5 shows fast parallel algorithms for texture
compression using the maximum likelihood estimate of parameters.
Conclusions are given in Section 6.



Next: Parallel Algorithm Analysis
Up: Scalable Data Parallel Algorithms
Previous: Scalable Data Parallel Algorithms
David A. Bader
dbader@umiacs.umd.edu
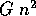 arithmetic operations
per iteration for an image of size
arithmetic operations
per iteration for an image of size 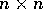 with G gray levels.
The implementations known to the authors are slow and operate on
images of size
with G gray levels.
The implementations known to the authors are slow and operate on
images of size 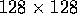 or smaller. Recently, a parallel
implementation has been developed on a DAP 510 computer
[21]. However, the DAP requires the structure of the
algorithms to match its topology, and hence the corresponding
algorithms are not as machine-independent as the algorithms described
in this paper. In addition, we show that our algorithms are scalable
in machine size and problem size.
or smaller. Recently, a parallel
implementation has been developed on a DAP 510 computer
[21]. However, the DAP requires the structure of the
algorithms to match its topology, and hence the corresponding
algorithms are not as machine-independent as the algorithms described
in this paper. In addition, we show that our algorithms are scalable
in machine size and problem size.
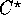 , data-parallel C, Fortran 90, Fortran D, and
CM Fortran. All our algorithms are scalable in terms of the number of
processors and the size of the problem. All the algorithms described
in this paper have been implemented and thoroughly tested on a
Connection Machine CM-2 and a Connection Machine CM-5.
, data-parallel C, Fortran 90, Fortran D, and
CM Fortran. All our algorithms are scalable in terms of the number of
processors and the size of the problem. All the algorithms described
in this paper have been implemented and thoroughly tested on a
Connection Machine CM-2 and a Connection Machine CM-5.
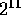 Sprint nodes are
configured as an 11-dimensional hypercube. See
Figure
Sprint nodes are
configured as an 11-dimensional hypercube. See
Figure 
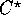 . In the SPMD model, each processing node executes a
portion of the same program, but local memory and machine state can
vary across the processors. The SPMD model efficiently simulates the
data parallel SIMD model normally associated with massively parallel
programming. References [
. In the SPMD model, each processing node executes a
portion of the same program, but local memory and machine state can
vary across the processors. The SPMD model efficiently simulates the
data parallel SIMD model normally associated with massively parallel
programming. References [