FAST OPTIMAL BANDWIDTH ESTIMATION FOR UNIVARIATE KDE - CODE
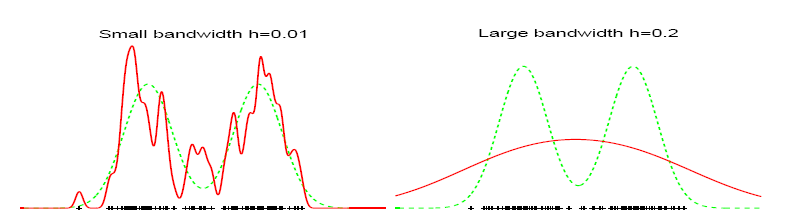
Efficient use of Kernel density estimation (KDE) requires the optimal selection of the smoothing parameter called the bandwidth h of the kernel. For a practical implementation of KDE the choice of the bandwidth h is very important. Small h leads to an estimator with small bias and large variance. Large h leads to a small variance at the expense of increase in bias. The bandwidth h has to be chosen optimally.

The most successful among all the current methods, both empirically and theoretically, is the solve-the-equation plug-in method. However this is computationally very expensive and scales as O(N^2). The code given here computes the same in O(N) time at the expense of reduced precision, which can be arbitrary.
The speedup is achieved based on a computationally efficient epsilon-exact approximation algorithm for the univariate Gaussian kernel based density derivative estimation. It computes the following sum at M points in O(M+N) time. The same code can be used for very fast univariate KDE. Note that r=1 corresponds to the KDE.
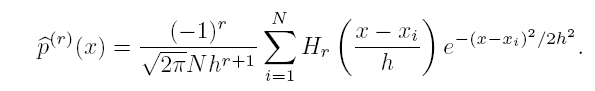
The estimation of the density derivative also comes up in various other applications like estimation of modes and inflexion points of densities and estimation of the derivatives of the projection index in projection pursuit algorithms.
The code is written in C++ with a MATLAB wrapper. I have provided the compiled dll files for windows platform. For other OS or if you have problems with the dlls you will have to recompile the C++ source code files provided. I would be interested to know if you used it any application.
Download:
[compiled dlls for windows] [ C++ source code ]
Publications:
Fast optimal bandwidth selection for kernel density estimation. Vikas C. Raykar and Ramani Duraiswami, In Proceedings of the sixth SIAM International Conference on Data Mining, Bethesda, April 2006, pp. 524-528. [paper] [brief slides] [bib]
Very fast optimal bandwidth selection for univariate kernel density estimation. Vikas C. Raykar and Ramani Duraiswami, CS-TR-4774, Department of computer science, University of Maryland, Collegepark. [abstract] [TR] [slides] [bib]
References:
S.J. Sheather and M.C. Jones. 'A reliable data-based bandwidth selection method for kernel density estimation' J. Royal Statist. Soc. B, 53:683 690, 1991.
Copyright Information:
The code was written by Vikas C. Raykar and is copyrighted under the Lesser GPL.
Copyright (C) 2006 Vikas C. Raykar
This program is free software; you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation; version 2.1 or later. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details. You should have received a copy of the GNU Lesser General Public License along with this program; if not, write to the Free Software Foundation, Inc., 59 Temple Place - Suite 330, Boston, MA 02111-1307, USA. The author may be contacted via email at: vikas (at) cs (.) umd (.) edu.
|
Input |
|
|
N |
number of source points. |
|
X |
1 x N vector of N source points. |
| epsilon | the desired error. |
|
Output |
|
| h | AMISE optimal bandwidth. |
|
List of Core Functions |
|
|
slow_univariate_bandwidth_estimate_STEPI fast_univariate_bandwidth_estimate_STEPI
|
AMISE optimal bandwidth estimation for univariate kernel density estimation using the Sheather Jones Solve-the-equation plug-in method. |
| UnivariateDensityDerivative | Direct implementation of the kernel density derivative estimate based on the Gaussian kernel. |
| FastUnivariateDensityDerivative | Fast implementation of the r th kernel density derivative estimate based on the Gaussian kernel. |
|
Utilities |
|
| example | Example program. |
| marron_wand_normal_mixtures |
This
function returns the actual density and samples from the 15 normal
mixture densities used by Marron and Wand. J. S. Marron and M. P. Wand 'Exact Mean Integrated Squared Error' The Annals of Statistics, 1992, Vol. 20, No. 2, 712-73 |
Last updated on 10/27/2006.