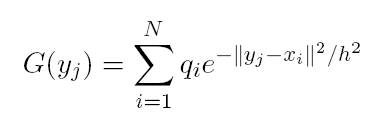
IMPROVED FAST GAUSS TRANSFORM Code

!! Latest version (faster and easier to use) of the code now available at FIGTree

Evaluating sums of multivariate Gaussian kernels (known as the discrete Gauss transform in the scientific computing literature) is a key computational task in many problems in computational statistics and machine learning. The computational complexity to evaluate the discrete Gauss transform at M target points due to N source points scales as O(MN). This makes the computation for large scale problems prohibitively expensive. The Improved Fast Gauss Transform (IFGT) is an epsilon-exact approximation algorithm that reduces the computational complexity to O(M + N), at the expense of reduced precision, which however can be arbitrary. The IFGT shows better scaling with dimensionality than the FGT.

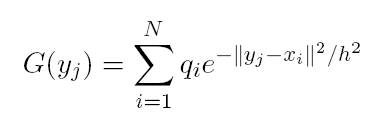
The code is written in C++ with a MATLAB wrapper. I have provided the compiled dll files for windows platform. For other OS you will have to recompile the C++ files. Read the user manual ( and maybe skim the TR ) before proceeding. I would be interested to know if you used it any application.

Fast computation of sums of Gaussians in high dimensions. Vikas C. Raykar, C. Yang, R. Duraiswami, and N. Gumerov, CS-TR-4767, Department of computer science, University of Maryland, CollegePark. [abstract] [TR] [slides] [bib]

The improved fast Gauss Transform with applications to machine learning. Vikas C. Raykar and Ramani Duraiswami, Presented at the NIPS 2005 workshop on Large scale kernel machines. [slides] [video]

Efficient Kernel Machines Using the Improved Fast Gauss Transform. Changjiang Yang, Ramani Duraiswami, and Larry Davis, In Advances in Neural Information Processing Systems, Volume 17, pages 1561-1568, 2005. [paper] [bib]

This program is free software; you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation; version 2.1 or later. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details. You should have received a copy of the GNU Lesser General Public License along with this program; if not, write to the Free Software Foundation, Inc., 59 Temple Place - Suite 330, Boston, MA 02111-1307, USA. The author may be contacted via email at: vikas (at) umiacs (.) umd (.) edu and cyang (at) sarnoff (.) com.

Input
d	data dimensionality.
N	number of source points.
M	number of target points.
h	bandwidth of the Gaussian kernel.
X	d x N matrix of N source points in d dimensions.
Y	d x M matrix of M target points in d dimensions.
q	1 x N vector of the source strengths.
epsilon	the desired error.
IFGT parameters [ automatically chosen ]
K	number of clusters.
p_max	maximum truncation number
r	cutoff radius
Output
G_IFGT	1 x M vector of the the evaluated IFGT.
List of Core Functions
ImprovedFastGaussTransformChooseParameters	Returns the number of clusters K, the maximum truncation number p_max, and the cutoff radius r.
ImprovedFastGaussTransformChooseTruncationNumber	Given the cluster radius, returns the required truncation number p_max.
KCenterClustering	Implementation of the farthest point clustering algorithm. This is the O(N logK) version.
ImprovedFastGaussTransform	Given the space subdivison results and the parameters computes the IFGT.
DataAdaptiveImprovedFastGaussTransform	Version of the IFGT where the truncation number for each source point is different.
IFGT	A wrapper function which combines all the above. Just provide the accuracy epsilon.
Utilities
GaussTransform	Direct implementation.
example	Example program to illustrate the use of the IFGT.
generate_multiple_gaussians	Generates N samples in d dimensions from G gaussians
plot_clusters	Pretty plot of the results of the clustering procedure. Plots only for two and three dimensions.