


Next: Radix Sort Algorithm
Up: Parallel Integer Sorting
Previous: Parallel Integer Sorting
We start by describing the counting sort algorithm used to sort on
individual blocks of the keys. The Counting Sort algorithm sorts
n integers in the range 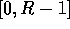 by using R counters to
accumulate the number of keys equal to i in bucket
by using R counters to
accumulate the number of keys equal to i in bucket 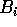 , for
, for 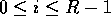 , followed by determining the rank of the each
element. Once the rank of each element is known, we can use our
h-relation personalized communication to move each element into the
correct position; in this case
, followed by determining the rank of the each
element. Once the rank of each element is known, we can use our
h-relation personalized communication to move each element into the
correct position; in this case 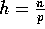 . Counting Sort is a
stable sorting routine, that is, if two keys are identical,
their relative order in the final sort remains the same as their
initial order.
. Counting Sort is a
stable sorting routine, that is, if two keys are identical,
their relative order in the final sort remains the same as their
initial order.
In a practical integer sorting problem, we expect 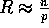 . The pseudocode for our Counting Sort algorithm uses six
major steps and is as follows.
. The pseudocode for our Counting Sort algorithm uses six
major steps and is as follows.
- Step (1): For each processor i, count the frequency of
its
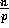 keys; that is, compute
keys; that is, compute 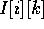 , the number of
keys equal to k, for
, the number of
keys equal to k, for 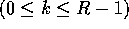 .
.
- Step (2): Apply the transpose primitive to the I
array using the block size
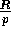 . Hence, at the end of this
step, each processor will hold
. Hence, at the end of this
step, each processor will hold 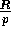 consecutive rows of I.
consecutive rows of I.
- Step (3): Each processor locally computes the prefix-sums
of its rows of the array I.
- Step (4): Apply the (inverse) transpose primitive
to the R corresponding prefix-sums augmented by the total count
for each bin. The block size of the transpose primitive is
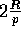 .
.
- Step (5): Each processor computes the ranks of local elements.
- Step (6): Perform a personalized communication of keys to
rank location using our h-relation algorithm for
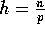 .
.
The analysis of our counting sort algorithm is as follows.
Steps (1), (3), and (5) execute in O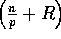 local computation time with no communication. Steps (2),
(4), and (6) are communication supersets and have the following
analysis. Steps (2) and (4) are the transpose
primitive with block sizes
local computation time with no communication. Steps (2),
(4), and (6) are communication supersets and have the following
analysis. Steps (2) and (4) are the transpose
primitive with block sizes 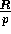 and
and 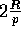 and hence
result in O
and hence
result in O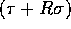 communication. Step (6) uses
the personalized communication primitive for n elements distributed
equally across p processors. Because this routing is a permutation
communication. Step (6) uses
the personalized communication primitive for n elements distributed
equally across p processors. Because this routing is a permutation
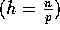 , it has the following complexity
, it has the following complexity
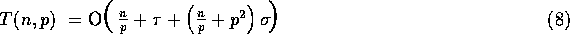
provided that 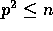 . Thus, the overall complexity of our
Counting Sort algorithm is given by
. Thus, the overall complexity of our
Counting Sort algorithm is given by
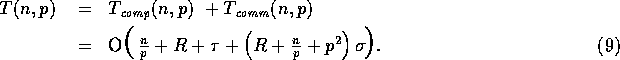
Notice that an obvious lower bound to sort the integers is

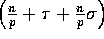 , and hence our algorithm
is asymptotically optimal when
, and hence our algorithm
is asymptotically optimal when 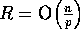 and
and 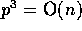 .
.



Next: Radix Sort Algorithm
Up: Parallel Integer Sorting
Previous: Parallel Integer Sorting
David A. Bader
dbader@umiacs.umd.edu
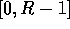 by using R counters to
accumulate the number of keys equal to i in bucket
by using R counters to
accumulate the number of keys equal to i in bucket 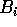 , for
, for 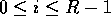 , followed by determining the rank of the each
element. Once the rank of each element is known, we can use our
h-relation personalized communication to move each element into the
correct position; in this case
, followed by determining the rank of the each
element. Once the rank of each element is known, we can use our
h-relation personalized communication to move each element into the
correct position; in this case 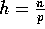 . Counting Sort is a
stable sorting routine, that is, if two keys are identical,
their relative order in the final sort remains the same as their
initial order.
. Counting Sort is a
stable sorting routine, that is, if two keys are identical,
their relative order in the final sort remains the same as their
initial order.
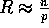 . The pseudocode for our Counting Sort algorithm uses six
major steps and is as follows.
. The pseudocode for our Counting Sort algorithm uses six
major steps and is as follows.
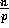 keys; that is, compute
keys; that is, compute 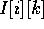 , the number of
keys equal to k, for
, the number of
keys equal to k, for 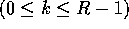 .
.
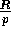 . Hence, at the end of this
step, each processor will hold
. Hence, at the end of this
step, each processor will hold 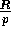 consecutive rows of I.
consecutive rows of I.
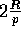 .
.
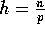 .
.
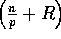 local computation time with no communication. Steps (2),
(4), and (6) are communication supersets and have the following
analysis. Steps (2) and (4) are the transpose
primitive with block sizes
local computation time with no communication. Steps (2),
(4), and (6) are communication supersets and have the following
analysis. Steps (2) and (4) are the transpose
primitive with block sizes 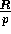 and
and 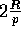 and hence
result in O
and hence
result in O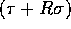 communication. Step (6) uses
the personalized communication primitive for n elements distributed
equally across p processors. Because this routing is a permutation
communication. Step (6) uses
the personalized communication primitive for n elements distributed
equally across p processors. Because this routing is a permutation
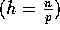 , it has the following complexity
, it has the following complexity
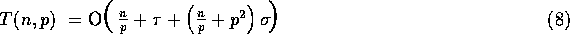
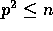 . Thus, the overall complexity of our
Counting Sort algorithm is given by
. Thus, the overall complexity of our
Counting Sort algorithm is given by
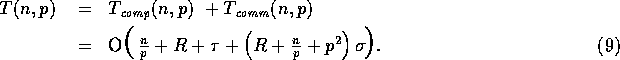

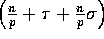 , and hence our algorithm
is asymptotically optimal when
, and hence our algorithm
is asymptotically optimal when 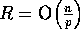 and
and 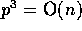 .
.