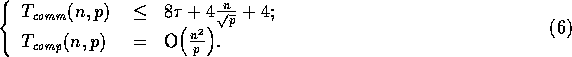Next:  -Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images
-Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images
Most common enhancement filters will smooth the interior of regions at
the cost of the edges, or find edges while introducing intrinsic error
on previously homogeneous regions. However, the Symmetric Neighborhood
Filter (SNF) is an edge-preserving smoothing filter, meaning that it
performs well for both edge sharpening and region flattening. The SNF
is a convergent filter which can be run for a predetermined number of
iterations, or until a percentage of the image pixels are fixed in
grey level. A variety of SNF operators have been studied, and we chose
a single parameter version which has been shown to perform well.
Previous parallel implementations of the SNF have been based around
special purpose image processing platforms, including data parallel
SIMD machines such as the TMC CM-2 and the MasPar MP-1 ([30]\
and [31]), video-rate VLSI implementations ([32]),
pipelined computers ([19]), and systolic linear arrays such
as the Warp ([2], [37], and [38]).
A useful data movement needed for this  local SNF filter
is the fetching of tile-based ghost cells ([15],
[43]) which contain shadow copies of neighboring tiles'
pixel borders. These ghost cells are used in the selection process
when recalculating our tile's border. Suppose each tile of the image
allocated to a processor is
local SNF filter
is the fetching of tile-based ghost cells ([15],
[43]) which contain shadow copies of neighboring tiles'
pixel borders. These ghost cells are used in the selection process
when recalculating our tile's border. Suppose each tile of the image
allocated to a processor is  pixels. We have four ghost
cell arrays, ghostN and ghostS which hold r pixels each,
and ghostW and ghostE which hold q pixels each. In
addition, four single pixel ghost cells for diagonal neighboring
pixels are ghostNW, ghostNE, ghostSE, and
ghostSW. An example of these ghost cells is pictured in
Figure 3.
pixels. We have four ghost
cell arrays, ghostN and ghostS which hold r pixels each,
and ghostW and ghostE which hold q pixels each. In
addition, four single pixel ghost cells for diagonal neighboring
pixels are ghostNW, ghostNE, ghostSE, and
ghostSW. An example of these ghost cells is pictured in
Figure 3.
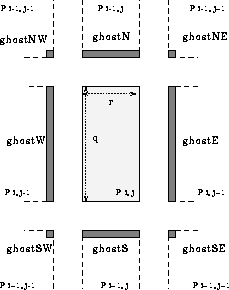
Figure 3: An example of Ghost Cells
The analysis for the prefetching of ghost cells is simple. We can
divide the prefetching into eight separate data movements, one for
each direction. Since each movement is a permutation, i.e. it has a
unique source and destination, it can be routed with little or no
contention.
The prefetching of the north and south ghost cell arrays
each take 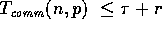 , the east and west ghost cell arrays
each take
, the east and west ghost cell arrays
each take 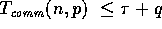 , and the diagonal four ghost cells
each take
, and the diagonal four ghost cells
each take 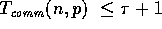 . Thus, the entire ghost cell
prefetching takes
. Thus, the entire ghost cell
prefetching takes
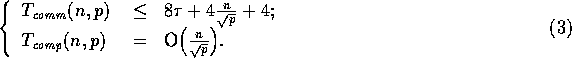
A second data movement needed for SNF is the reduction
operation. Each processor i has a data value, 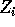 , and we need the
value of
, and we need the
value of 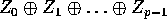 , where
, where 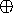 is any associative operator. Parallel computers can handle this
efficiently [7], and SPLIT-C implements this as a
primitive library function. A simple algorithm consists of p-1
rounds that can be pipelined [25]. Each processor
is any associative operator. Parallel computers can handle this
efficiently [7], and SPLIT-C implements this as a
primitive library function. A simple algorithm consists of p-1
rounds that can be pipelined [25]. Each processor 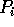 initializes a local sum to
initializes a local sum to 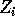 . During round r, each processors
then reads
. During round r, each processors
then reads 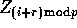 , for
, for 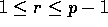 , and adds this
value to the local sum. Since these rounds can be realized with p-1
pipelined prefetch read operations, the resulting complexity is
, and adds this
value to the local sum. Since these rounds can be realized with p-1
pipelined prefetch read operations, the resulting complexity is

An SPMD algorithm for an iteration of SNF on Processor i:

For each iteration of the SNF operator on a p-processor machine, the
theoretical analysis is as follows. The complexities for Step 1 and
Step 4 are shown in (3) and
(4), respectively. Steps 2 and 3 are completely
local and take O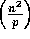 . Thus, for
. Thus, for 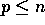 , the SNF complexities
are
, the SNF complexities
are
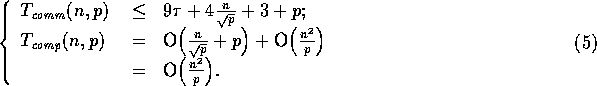
Figure 10 in Appendix B shows the convergence of
the SNF enhancement during the second phase of the smoothing filter.
As can be seen, there is a fast convergence of the pixels
asymptotically close to 100% fixed. Because fixed pixels are not
recalculated, the time per iteration quickly ramps down from
approximately 165 ms/iteration to 26 ms/iteration on a  TM image.
TM image.
The complexity of an iteration of the 1-Nearest Neighbor filter is simple, namely,
a fetch of ghost cells and one pass through the image tile on each
processor. The ghost cell analysis is given in (3),
and the update of pixels takes O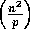 . Therefore, the 1-Nearest Neighbor \
algorithm has complexities
. Therefore, the 1-Nearest Neighbor \
algorithm has complexities
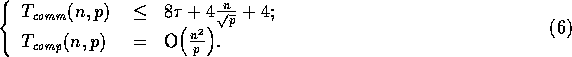



Next:  -Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images
-Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images
David A. Bader
dbader@umiacs.umd.edu
 local SNF filter
is the fetching of tile-based ghost cells ([15],
[43]) which contain shadow copies of neighboring tiles'
pixel borders. These ghost cells are used in the selection process
when recalculating our tile's border. Suppose each tile of the image
allocated to a processor is
local SNF filter
is the fetching of tile-based ghost cells ([15],
[43]) which contain shadow copies of neighboring tiles'
pixel borders. These ghost cells are used in the selection process
when recalculating our tile's border. Suppose each tile of the image
allocated to a processor is 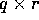 pixels. We have four ghost
cell arrays, ghostN and ghostS which hold r pixels each,
and ghostW and ghostE which hold q pixels each. In
addition, four single pixel ghost cells for diagonal neighboring
pixels are ghostNW, ghostNE, ghostSE, and
ghostSW. An example of these ghost cells is pictured in
Figure 3.
pixels. We have four ghost
cell arrays, ghostN and ghostS which hold r pixels each,
and ghostW and ghostE which hold q pixels each. In
addition, four single pixel ghost cells for diagonal neighboring
pixels are ghostNW, ghostNE, ghostSE, and
ghostSW. An example of these ghost cells is pictured in
Figure 3.
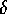 -Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images
-Connected Components of Greyscale Images
Up: Parallel Algorithms for Image Segmentation
Previous: Test Images

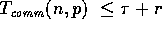 , the east and west ghost cell arrays
each take
, the east and west ghost cell arrays
each take 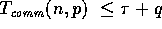 , and the diagonal four ghost cells
each take
, and the diagonal four ghost cells
each take 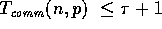 . Thus, the entire ghost cell
prefetching takes
. Thus, the entire ghost cell
prefetching takes
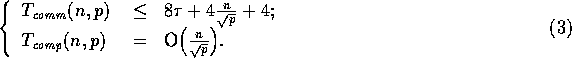
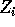 , and we need the
value of
, and we need the
value of 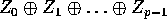 , where
, where 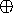 is any associative operator. Parallel computers can handle this
efficiently [
is any associative operator. Parallel computers can handle this
efficiently [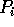 initializes a local sum to
initializes a local sum to 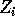 . During round r, each processors
then reads
. During round r, each processors
then reads 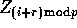 , for
, for 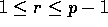 , and adds this
value to the local sum. Since these rounds can be realized with p-1
pipelined prefetch read operations, the resulting complexity is
, and adds this
value to the local sum. Since these rounds can be realized with p-1
pipelined prefetch read operations, the resulting complexity is


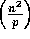 . Thus, for
. Thus, for 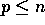 , the SNF complexities
are
, the SNF complexities
are
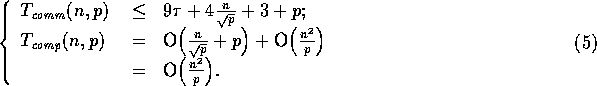
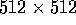 TM image.
TM image.
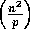 . Therefore, the 1-Nearest Neighbor \
algorithm has complexities
. Therefore, the 1-Nearest Neighbor \
algorithm has complexities