

Next: Mean Shift Analysis and
Up: Research Summary
Previous: Research Summary
The fast multipole method has been called one of the ten most
significant numerical algorithms discovered in the 20th century
(along with algorithms such as the fast Fourier transform), and
won its inventors, V. Rokhlin and L. Greengard, the 2001 Steele
prize, in addition to getting Greengard the ACM best dissertation
award. The algorithm allows the product of particular dense
matrices with a vector to be evaluated approximately (to a
specified precision) in
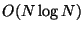 operations, when direct
multiplication requires
operations, when direct
multiplication requires 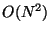 operations. For extremely large
problems, the gain in efficiency and memory can be very
significant, and enables the use of more powerful modeling
approaches that may have been discarded as computationally
infeasible in the past.
operations. For extremely large
problems, the gain in efficiency and memory can be very
significant, and enables the use of more powerful modeling
approaches that may have been discarded as computationally
infeasible in the past.
The fast Gauss transform (FGT) introduced by Greengard and Strain
is an important variant of the more general fast multipole method.
While the fast multipole method has been successfully in many
mathematics and physics domains, the fast Gauss transform is
widely applied in many applications of computer vision and pattern
recognition.
While the original FGT has been successfully applied to problem in
low dimensional spaces, it suffers from two serious defects in
higher dimensional spaces:
- The exponential growth of complexity with dimensionality.
- The use of the box data structure in the FGT is inefficient in higher
dimensions.
To overcome the difficulties of FGT in higher dimensional spaces,
we proposed a new multivariate Taylor expansion whose complexity
is asymptomatically polynomial order. To adaptively fit the
density of points, we use 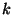 -center algorithm (a.k.a.
farthest-point algorithm) to subdivide the space. The complexity
of
-center algorithm (a.k.a.
farthest-point algorithm) to subdivide the space. The complexity
of 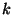 -center algorithm is
-center algorithm is
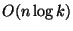 . The result of
. The result of
 -center algorithm is shown by the following Java demonstration.
We also give a relatively simple error bound of our improved fast
Gauss transform.
-center algorithm is shown by the following Java demonstration.
We also give a relatively simple error bound of our improved fast
Gauss transform.
The improved fast Gauss transform has been
successfully applied to many applications, such as mean shift
algorithm, realtime object tracking, efficient kernel density
estimation, kernel machines, image segmentation, etc.
References
- C. Yang, R. Duraiswami and L. Davis. Efficient Kernel Machines Using the Improved Fast Gauss Transform. In Advances in Neural Information Processing Systems 16, 2004.
- C. Yang, R. Duraiswami, N. Gumerov and L. Davis. Improved Fast Gauss Transform and Efficient Kernel Density Estimation, In IEEE International Conference on Computer Vision, pages 464-471, 2003.
- C. Yang, R. Duraiswami, A. Elgammal and L. Davis. Real-Time Kernel-Based Tracking in Joint Feature-Spatial Spaces. Technical Report CS-TR-4567, Dept. of Computer Science, University of Maryland, College Park, 2004.
- C. Yang, R. Duraiswami and N. Gumerov. Improved Fast Gauss Transform. Technical Report CS-TR-4495, Dept. of Computer Science, University of Maryland, College Park, also submitted SIAM Sci. Comput. for publication, 2003.


Next: Mean Shift Analysis and
Up: Research Summary
Previous: Research Summary
Changjiang Yang
2005-03-01