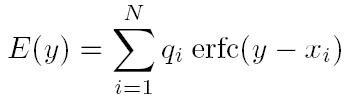Direct computation of the weighted sum of N complementary error functions at M points scales as O(MN). The following code computes the same extremely fast to epsilon-precision in O(M + N). For example for N = M = 51,200 points while the direct evaluation takes around 17.26 hours the fast evaluation requires only 4.29 seconds with an error of around 1e-10.
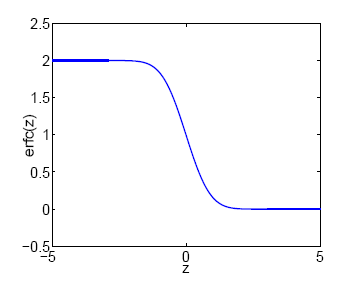
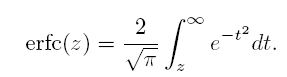
The code is written in C++ with a MATLAB wrapper. I have provided the compiled dll files for windows platform. For other OS you will have to recompile the C++ files. Read the technical report before proceeding. I would be interested to know if you used it any application. There is also a bit slower MATLAB version of the code.
Download: [ C++ source code along with dlls ]
Publications:
Fast weighted summation of erfc functions. Vikas C. Raykar, R. Duraiswami, and B. Krishnapuram, CS-TR-4848, Department of computer science, University of Maryland, CollegePark. [abstract] [TR] [slides] [bib]
We have embedded the above fast summation in an optimization algorithm for learning ranking functions.
A fast algorithm for learning large scale preference relations. Vikas C. Raykar, Ramani Duraiswami, and Balaji Krishnapuram, In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics, San Juan, Peurto Rico, March 2007, pp. 385-392. [paper] [slides] [bib] [ More details can be found in CS-TR-4848 ] [oral presentation] [code]
Copyright Information The code was written by Vikas C. Raykar and is copyrighted under the Lesser GPL:
Copyright (C) 2007 Vikas C. Raykar
This program is free software; you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation; version 2.1 or later. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details. You should have received a copy of the GNU Lesser General Public License along with this program; if not, write to the Free Software Foundation, Inc., 59 Temple Place - Suite 330, Boston, MA 02111-1307, USA. The author may be contacted via email at: vikas (at) umiacs (.) umd (.) edu.